Hoeffding不等式

下面有一个罐子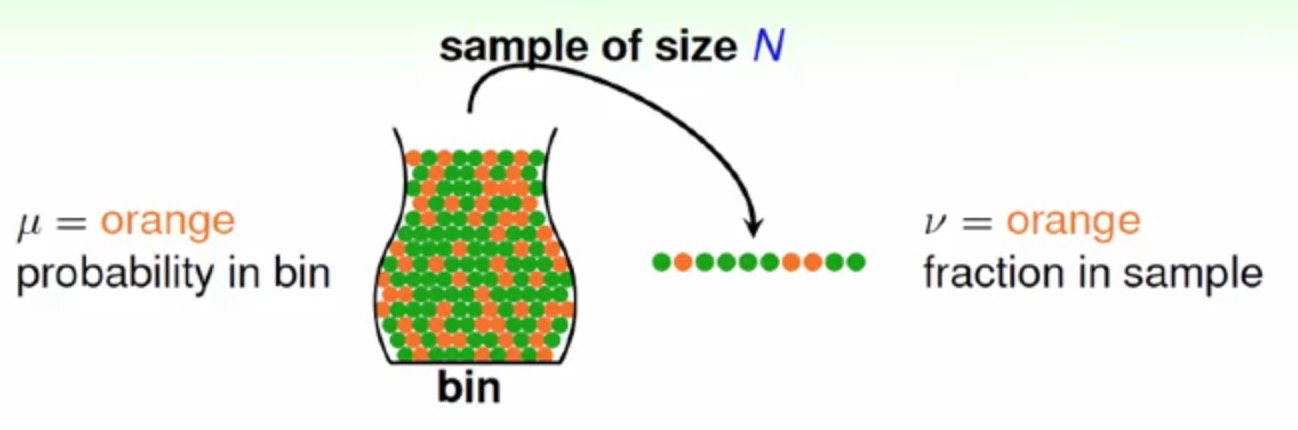

罐子中的球是橙色的概率是μ，现从罐子中取出N个数量的球作为样本，其中样本中含橙色求的概率是ν，那么μ和ν是否会接近呢？

这里有一个叫做Hoeffding不等式可以来解释该问题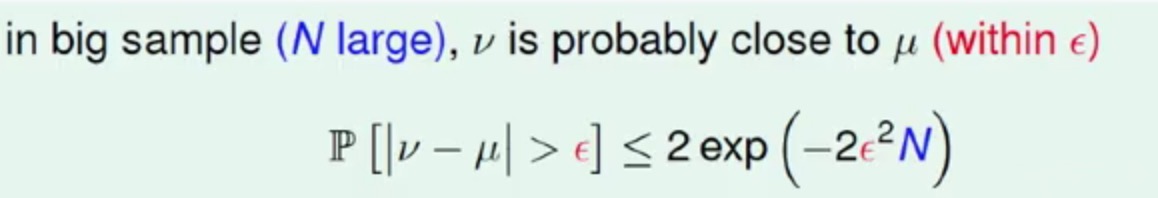

大致的表述就是μ与ν之差的绝对值小于ξ的概率为2exp(-2ξ2N)（这个概率也叫坏事发生的几率，林老师的叫法真的很kwy ^_^）,ξ越小，μ与ν越接近，其概率：

• ξ越大，坏事发生的几率越小，但是ξ真的很大时，坏事发不发生已经么啥意义了-_-
• N越大，坏事发生的几率越小，μ与ν会越来越接近,所以取样时大一点可以增加准确率.

  将N取到总得数量，那就是μ=ν

这里的‘μ=ν’的状态问题称为probably approximately correct（PAC）问题，表示大概差不多是对的。 

所以，取的样本够大的时候，未知的μ可以从已知的ν推论出来，并且他们俩是类似的。

应用于Learning

假设当前一个学习算法的最终的实际假设是f(x)(一般是未知的)，其h(x)表示采样了之后的假设，其yn为对应样本上的目标值。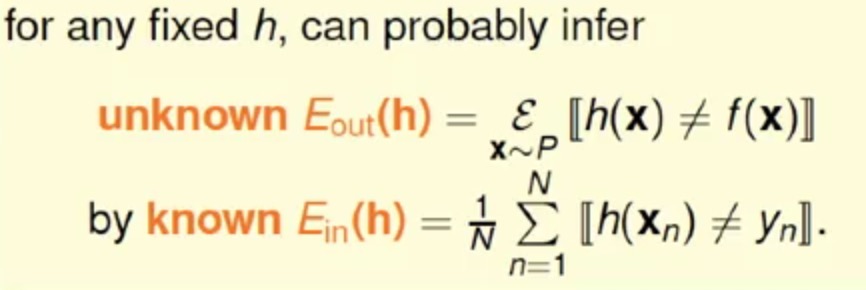

这里的Eout(h)和Ein(h)正好就是对应上一节的μ=ν
Hoeffding不等式同样是适用于Learning问题

所以在Learning的时候，可以从Ein(h)来推断出Eout(h)，也就是我们的Learning目的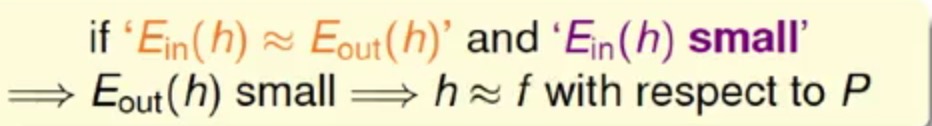

上面如果能得到一个很小的Ein(h)，当然是皆大欢喜，此时g’=f’(g,f分别对应h(x)和f(x)对应的线/假设)，但是要知道其实在算法上其实有很多h可以选，那时候选择到得Ein(h)比较大得时候，那就比较悲催了，所以真实地学习应该是：

像PLA一样选一根最优的线。

Hoeffding不等式只能保证Ein(h)和Eout(h)会有一个较大的几率说明他俩是相似的，但是无法保证在非常多得假设下(h(x))下，Ein(h)的值时比较小，那如果最终Ein(h)的值比较大，那么最终学习的算法就不好了，这个也叫做踩雷过程(这也可能使由于样本原因造成的)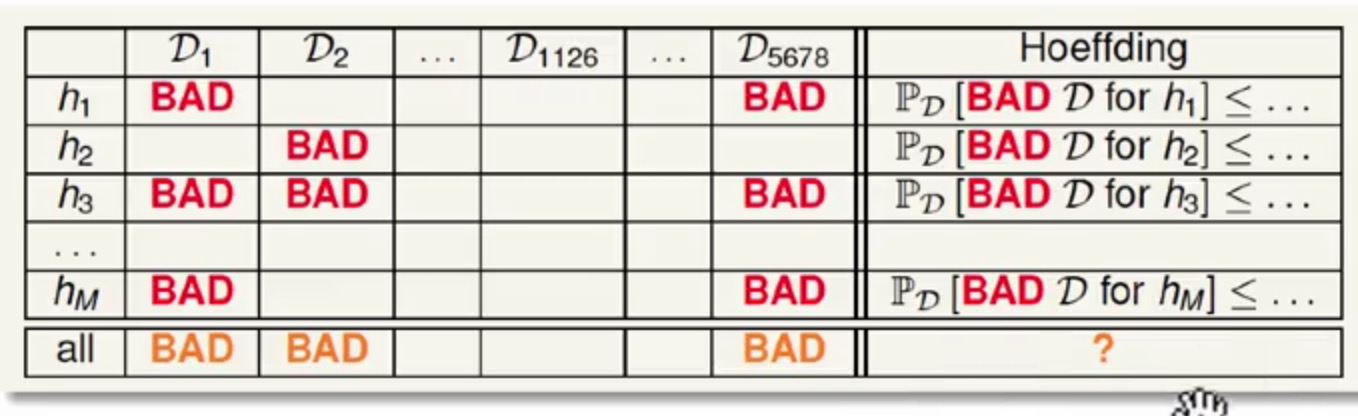

现在有M个假设，同时数据集可能会有表中的几个样本采样出来，BAD标志就是表示当前假设下在对应的样本上是踩雷了(Ein(h))很大

但是学习算法最希望的就是自由的选择具体假设下，能够得到具体的BAD几率

这里可以使用联合bound的方式来求总体的BAD几率

从式子中可以发现最终的几率是加上了M的Hoeffding不等式几率

关于M的无限大问题

上面知道M表示所有假设，而比如在PLA问题中可以了解到其实平面上会有无数条线，也就是无数条假设(M)，那这样其实上一小节中计算出来的几率会变无限大吗？那不是白搭了嘛-_-

这里先换个思路想一下：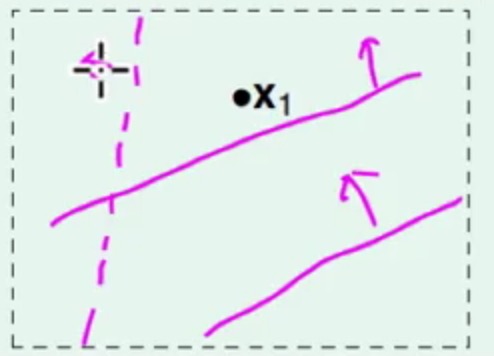

上图的PLA只有一个点，上面画了可能存在的三条线，其实可以发现这两条实线是一个含义，这里只有两种线而已(一虚一实)
再者看一下两个点的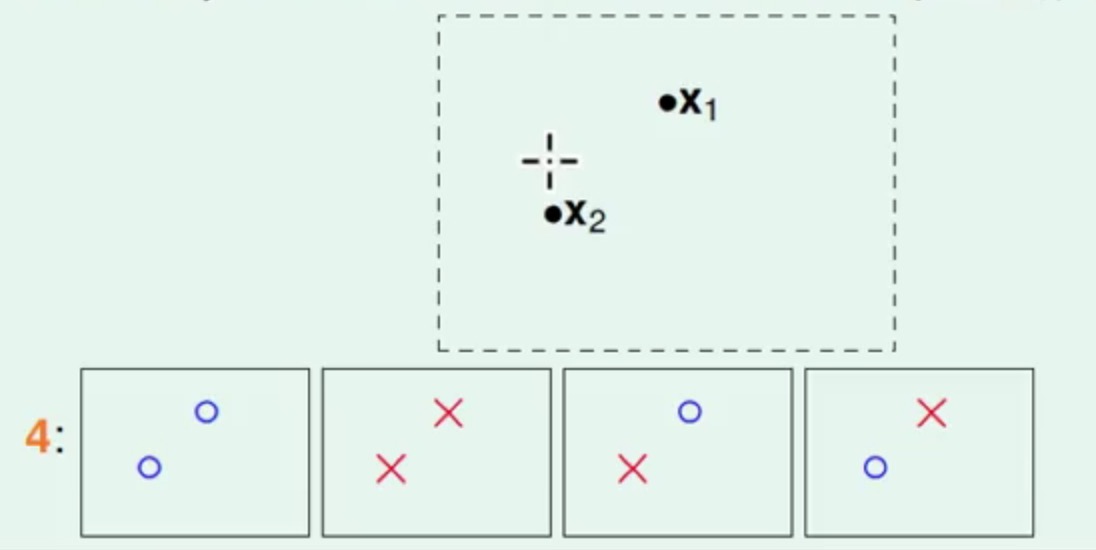

它就会有四种线
还有看一下三个点得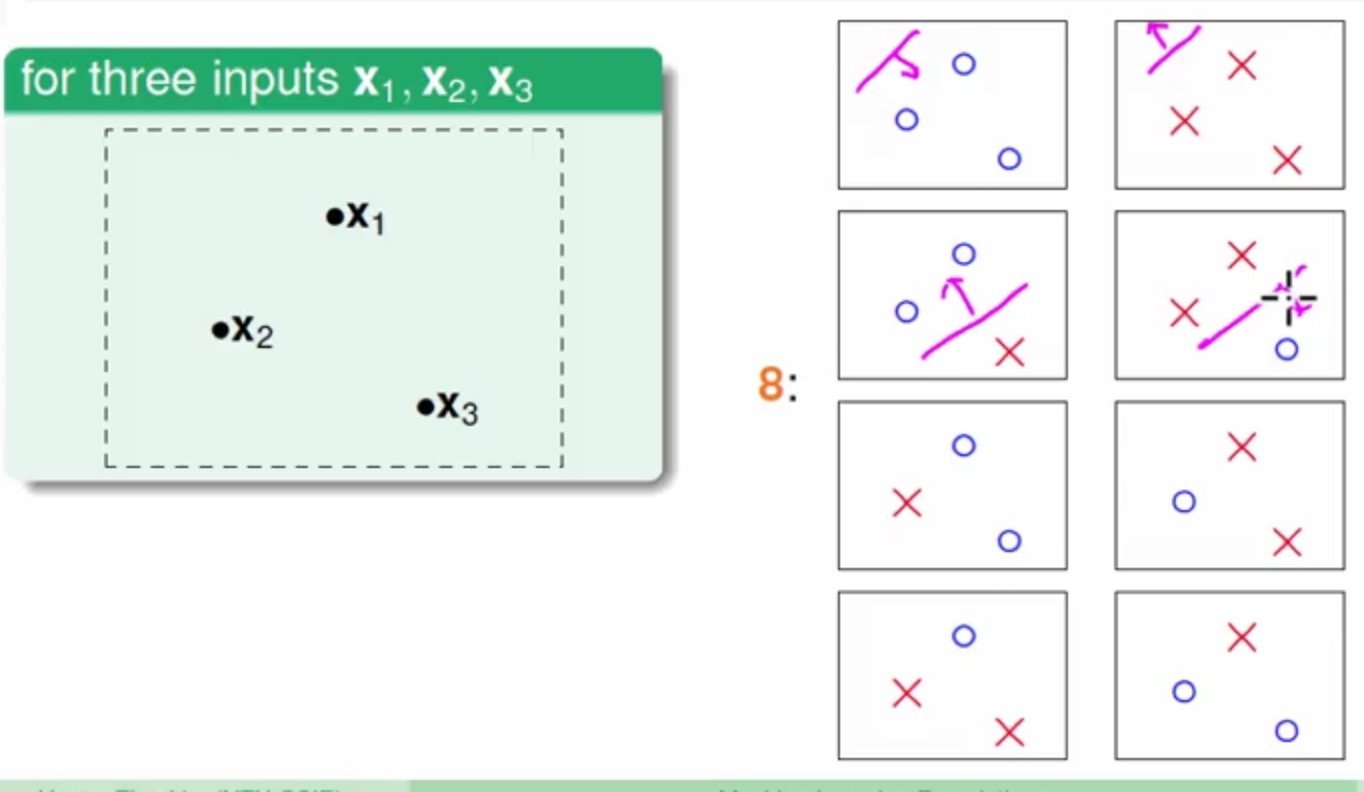

它最终会有八种线(其实如果这三个点成一条直线或者重叠在一个点上面的话不会有这么多)
再推演下去会有这么一个规律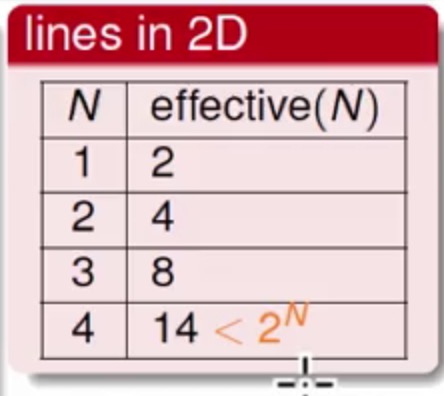

在二维上，平面上划分这些点的种类数总是小于2^N

现在假设使用mH(N)来表示N个点的时候可能出现的最大分类线种数dichotomies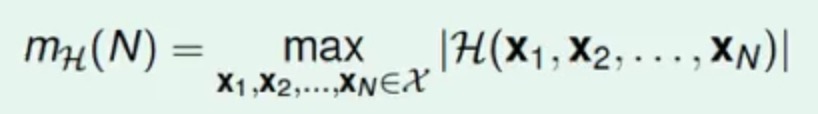

那么这个mH(N)的上界就是2^N，这个函数也叫做成长函数(Growth Function)

现在综合看一下其他维度的成长函数值:

• 一维的二分类 N+1
  
• 一维的二分类（使用中间区间分开） 1/2*N2+1/2*N+1
  
• 可以绕成一圈的凸集合 2N
  

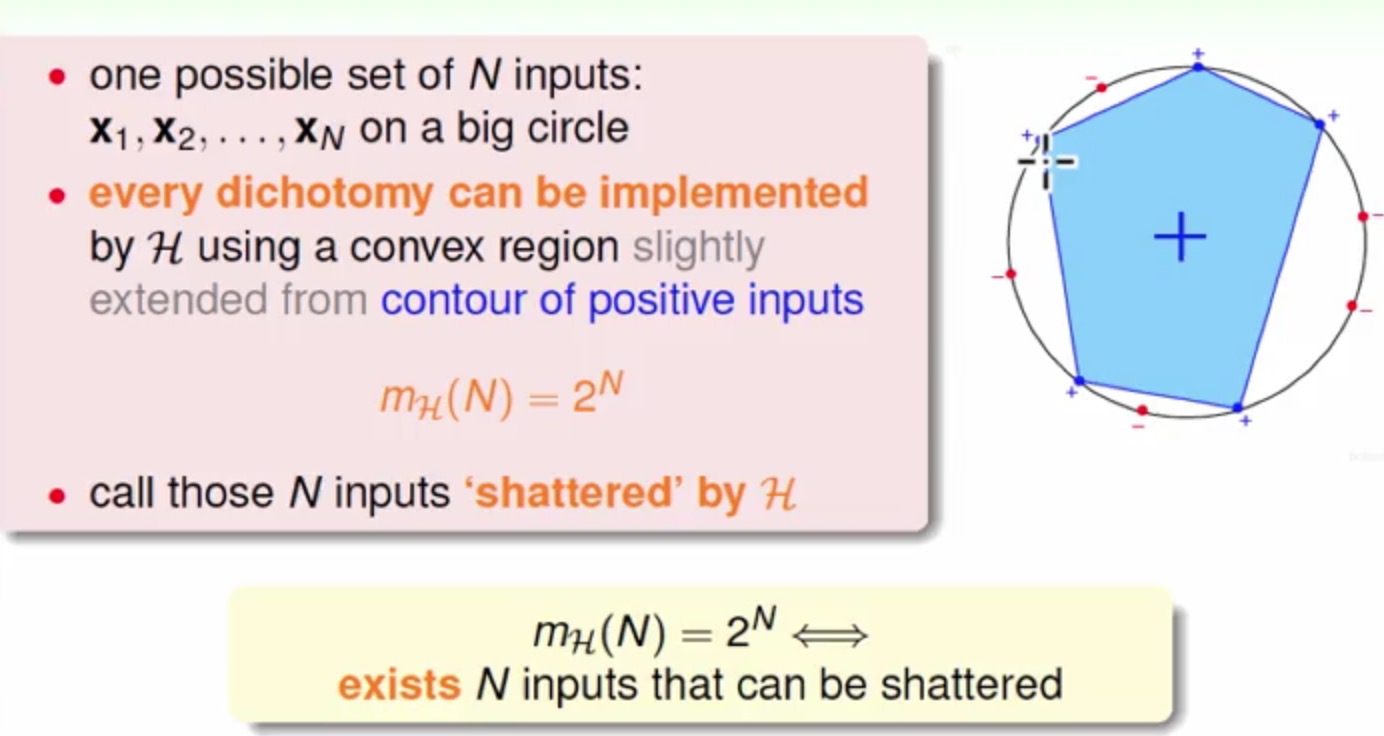
  这里类似凸集的情况下N个点可能hold住2N分类面的情况叫shattered

那么好了，如果mH(N)能直接取代M,同时mH(N)为多项式的话，N越大，那个这个upbound会越来越小，或者接近于0

现在来看一个break point的概念

表示第一个无法shattered的点,比如在上面lines in 2D的图里面在3个点的时候最多有8条线(2^3)，正好是shattered,但是到了4个点的时候最多只有14条线，此时就无法shattered,故4就是2D-PLA的break point，同理

那么这里可以通过推算最终可以知道mH(N)=O(N^(k-1))（具体证明要看看下一个视频VC维相关）,其中这里的k表示break point，这样就可以说上上上面的mH(N)是有限的，关于如果代替M的问题还得看下个分解。

总结

所以当算法的该含有一个有限的break point的时候，并且采样的资料量N够多，就可以保证找到一个Ein(h)最小的时候，得到最小的Eout(h),也就是说明Learning的可行性。（好绕）^_^

参考

• 《台湾国立大学-机器学习基石》第四讲
• 《台湾国立大学-机器学习基石》第五讲
• 《台湾国立大学-机器学习基石》第六讲

配图均来自《台湾国立大学-机器学习基石》

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。